1 PCA算法原理
主成分分析,顾名思义,就是分析出数据里最主要的成分,用来代替原始数据。我们希望通过空间坐标变换的方式,把原始数据映射到一个新的坐标系中,其中第一主轴(主成分)所包含的信息最多,也就是尽可能多地保留了原始数据的特征。为了更直观地理解,我们来看一个比较简单的例子。假设现在有10位同学在5门课程上的成绩:
| 科目 | A | B | C | D | E | F | G | H | I | J |
|---|---|---|---|---|---|---|---|---|---|---|
| 数学 | 95 | 91 | 88 | 70 | 75 | 80 | 78 | 65 | 85 | 90 |
| 物理 | 90 | 87 | 85 | 65 | 70 | 76 | 73 | 60 | 80 | 88 |
| 历史 | 76 | 82 | 70 | 85 | 88 | 84 | 80 | 70 | 74 | 73 |
| 地理 | 78 | 78 | 75 | 80 | 82 | 79 | 81 | 73 | 77 | 76 |
| 生物 | 85 | 84 | 83 | 79 | 80 | 82 | 81 | 72 | 84 | 86 |
我们可以把这些数据看作一个 \( 5 \times 10\)的矩阵 \( \mathbf{X}\)每一列表示一位学生的成绩(样本),每一行表示一个科目的得分(特征):
$$ \mathbf{X} = \begin{bmatrix} 95 & 91 & 88 & 70 & 75 & 80 & 78 & 65 & 85 & 90 \\ 90 & 87 & 85 & 65 & 70 & 76 & 73 & 60 & 80 & 88 \\ 76 & 82 & 70 & 85 & 88 & 84 & 80 & 70 & 74 & 73 \\ 78 & 78 & 75 & 80 & 82 & 79 & 81 & 73 & 77 & 76 \\ 85 & 84 & 83 & 79 & 80 & 82 & 81 & 72 & 84 & 86 \end{bmatrix} $$
从直觉上来看,数学和物理成绩变化趋势非常一致,它们可能可以合并为一个主成分;历史和地理也存在较强相关性,可能对应另一个主成分;生物则可能与其他科目有一定交叉关联。主成分分析(PCA)所做的事情,就是自动找出这些“隐藏的组合维度”,并以更少的维度来表示原始数据。在这个例子中,我们原本有5个科目(即5维特征),但PCA可能只需2个主成分就能很好地近似地表示这些成绩差异。因此,我们可以利用PCA的这个特性来进行数据降维,合并一些维度所包含的信息。接下来我们就可以利用降维后得到的信息来评估每位同学的综合水平:
| 主成分 | A | B | C | D | E | F | G | H | I | J |
|---|---|---|---|---|---|---|---|---|---|---|
| 第一主成分(理科能力?) | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| 第二主成分(文科能力?) | ? | ? | ? | ? | ? | ? | ? | ? | ? | ? |
| … | … | … | … | … | … | … | … | … | … | … |
因此我们可以抽象出一般的问题,假设我们共有\( n\)数据,且每一个数据样本都是\( d\)的,我们希望将这\( n\)数据的维度从\( d\)缩减至\( d’\),同时希望这\( n\)\( d’\)的数据集尽可能地代表原始数据集。因此,主成分分析在机器学习中是一种常用的降维方法。以下有两种PCA的推导形式,包括基于最近重构性与基于最大可分性。
1.1 基于最近重构性
基于最近重构性,或者说基于最小投影距离,也就是说,每个样本点到降维后的样本点(超平面)的距离都尽可能相近。具体来说,它的目标是找到一个低维子空间,使得原始数据投影到这个子空间上的重建误差最小,即找到一个投影方向,使得所有数据点的重构误差的平方和最小。
给定数据集\( \mathbf{X}=[\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_{n}]\in \mathbb{R}^{d\times n}\)降维后再重构后的数据集为\( \mathbf{\hat{X}}=[\hat{\boldsymbol{x}}_1,\hat{\boldsymbol{x}}_2,\dots,\hat{\boldsymbol{x}}_{n}]\in \mathbb{R}^{d\times n}\)即降维后的数据点在原始坐标空间的表示),重建误差定义为原始数据点和它们在低维子空间上的投影之间的平方误差(相当于欧式平方距离)之和:$$ J = \| \mathbf{X} – \mathbf{\hat{X}} \|^2 = \sum_{i=1}^n \| \boldsymbol{x}_i – \hat{\boldsymbol{x}}_i \|^2 $$
若数据样本已经进行了中心化(防止位置偏移影响主轴信息),即\( \displaystyle \sum_{i=1}^n \boldsymbol{x}_i=\boldsymbol{0}\)投影变换后的 \( d’\)子空间使用原坐标系下的基向量表示为\( \mathbf{W}=[\boldsymbol{w}_1,\boldsymbol{w}_2,\dots,\boldsymbol{w}_{d’}]\in \mathbb{R}^{d\times d’}\) 其中\( \boldsymbol{w}_i\)标准正交向量基,即\( \|\boldsymbol{w}_i\|_2=1\)、\( \boldsymbol{w}_i^\top \boldsymbol{w}_j=0 (i\ne j)\),也即 \( \mathbf{W}^\top\mathbf{W} = \mathbf{I}\)为\( d’\times d’\)单位矩阵。
若仅保留\( d’\)主成分,也就是降维后(从\( d\)降到\( d’\)了!),样本点在该新的低维子空间中表示为\( \boldsymbol{z}_{i}=\mathbf{W}^\top \boldsymbol{x}_{i}=(z_{i1},z_{i2},\dots,z_{id’})^\top\)其中\( z_{ij}=\boldsymbol{w}_j^\top\boldsymbol{x}_i\)\( \boldsymbol{x}_i\)第\( j\)的数据。基于\( \boldsymbol{z}_{i}\)重构\( \hat{\boldsymbol{x}}_i\)则有:
$$\hat{\boldsymbol{x}}_i=z_{i1}\boldsymbol{w}_1+z_{i2}\boldsymbol{w}_2+\dots+z_{id’}\boldsymbol{w}_{d’}=\sum_{j=1}^{d’}z_{ij}\boldsymbol{w}_j=\mathbf{W}\boldsymbol{z}_i=\mathbf{W}\mathbf{W}^\top \boldsymbol{x}_{i}$$
,其中\( \mathbf{W}\mathbf{W}^\top\in \mathbb{R}^{d\times d}\)称为投影矩阵。(重构实际上就是将投影后的数据点在原始空间坐标系下表示出来!)
♪(^∀^●)ノ 接下来我们开始最小化重构误差:
$$\begin{align*}
\min J &= \min_{\mathbf{\hat{X}}} \sum_{i=1}^n \| \boldsymbol{x}_i – \hat{\boldsymbol{x}}_i \|^2=\min_{\mathbf{W},\mathbf{Z}} \sum_{i=1}^n \| \boldsymbol{x}_i – \mathbf{W} \boldsymbol{z}_i \|^2 \\
&= \min_{\mathbf{W},\mathbf{Z}} \sum_{i=1}^n \left(\boldsymbol{x}_i – \mathbf{W} \boldsymbol{z}_i)^\top (\boldsymbol{x}_i – \mathbf{W} \boldsymbol{z}_i\right) \\
&= \min_{\mathbf{W},\mathbf{Z}} \sum_{i=1}^n \left(\boldsymbol{x}_i^\top – \boldsymbol{z}_i^\top \mathbf{W}^\top)(\boldsymbol{x}_i – \mathbf{W} \boldsymbol{z}_i\right) \\&= \min_{\mathbf{W},\mathbf{Z}} \sum_{i=1}^n \Bigl(\underbrace{\boldsymbol{x}_i^\top\boldsymbol{x}_i}_{\text{常数}} \ \underbrace{- \boldsymbol{z}_i^\top \mathbf{W}^\top \boldsymbol{x}_i-\boldsymbol{x}_i^\top \mathbf{W} \boldsymbol{z}_i}_{\text{标量,转置相同可合并}}+\underbrace{\boldsymbol{z}_i^\top \mathbf{W}^\top\mathbf{W} \boldsymbol{z}_i}_{\mathbf{W}^\top\mathbf{W}=\mathbf{I}}\Bigr) \\&= \min_{\mathbf{W},\mathbf{Z}} \sum_{i=1}^n \left( – 2\boldsymbol{z}_i^\top \mathbf{W}^\top \boldsymbol{x}_i+\boldsymbol{z}_i^\top\boldsymbol{z}_i\right) \\&= \min_{\mathbf{W}} \sum_{i=1}^n \left( – 2(\mathbf{W}^\top \boldsymbol{x}_{i})^\top \mathbf{W}^\top \boldsymbol{x}_i+(\mathbf{W}^\top \boldsymbol{x}_{i})^\top\mathbf{W}^\top \boldsymbol{x}_{i}\right) \\&= \min_{\mathbf{W}} \sum_{i=1}^n -\boldsymbol{x}_{i}^\top\mathbf{W} \mathbf{W}^\top \boldsymbol{x}_i = \min_{\mathbf{W}}-\underbrace{\mathrm{Tr}\left(\mathbf{X}^\top\mathbf{W}\mathbf{W}^\top\mathbf{X} \right)}_{\text{根据迹的性质交换元素位置}}\\&= \max_{\mathbf{W}}\mathrm{Tr}\left(\mathbf{W}^\top\mathbf{X}\mathbf{X}^\top\mathbf{W} \right)\tag{1.1}\end{align*}$$
因此,优化目标就变成了在\( \mathbf{W}^\top\mathbf{W}=\mathbf{I}\)条件下,使得\( \mathrm{Tr}\left(\mathbf{W}^\top\mathbf{X}\mathbf{X}^\top\mathbf{W} \right)\)大化。
在带有约束的求极值情况,我们优先考虑使用拉格朗日乘数法:
$$\begin{align*} L(\mathbf{W}, \mathbf{\Lambda})&=\mathrm{Tr}\left(\mathbf{W}^\top\mathbf{X}\mathbf{X}^\top\mathbf{W} \right)-\mathrm{Tr}\left(\mathbf{\Lambda}^\top(\mathbf{W}^\top\mathbf{W}-\mathbf{I})\right) \end{align*}$$
其中,\( \mathbf{\Lambda}\)大小与\( \mathbf{W}^\top \mathbf{W}-\mathbf{I}\)全相同维度的对角矩阵(严格来说应该是对称矩阵,由于后续可以通过列空间正交旋转\( \mathbf{W}\)及让\( \mathbf{\Lambda}\)角化,目标值与约束均不变,为便于推导,直接令其为对角矩阵)。对两个变量求导,得:
$$\begin{align*}\frac{\partial L(\mathbf{W}, \mathbf{\Lambda})}{\partial \mathbf{W}}&=2\mathbf{X}\mathbf{X}^\top\mathbf{W}-\mathbf{W}(\mathbf{\Lambda}+\mathbf{\Lambda}^\top)=\boldsymbol{0} \\ \frac{\partial L(\mathbf{W}, \mathbf{\Lambda})}{\partial \mathbf{\Lambda}}&=\mathbf{W}^\top\mathbf{W}-\mathbf{I}=\boldsymbol{0} \end{align*} $$
因此有: $$\mathbf{X}\mathbf{X}^\top\mathbf{W}=\mathbf{W}\mathbf{\Lambda} \tag{1.2}$$
我们可以把\( \mathbf{W}\)\( \mathbf{\Lambda}\)展开,即\( \mathbf{W}=[\boldsymbol{w}_1,\boldsymbol{w}_2,\dots,\boldsymbol{w}_{d’}]\)、\( \mathbf{\Lambda}=\mathrm{diag}(\lambda_1,\lambda_2,\dots,\lambda_{d’})\),且由于\( \mathbf{X}\mathbf{X}^\top\)是实对称矩阵,必可对角化(所有特征值的代数重数=几何重数,即能找到\( d\)线性无关的特征向量,我们从中选取\( d’\)),因此有: $$\begin{align*} \mathbf{X}\mathbf{X}^\top\boldsymbol{w}_1&=\lambda_1 \boldsymbol{w}_1 \\ \mathbf{X}\mathbf{X}^\top\boldsymbol{w}_2&=\lambda_2 \boldsymbol{w}_2 \\&\vdots \\ \mathbf{X}\mathbf{X}^\top\boldsymbol{w}_{d’}&=\lambda_{d’} \boldsymbol{w}_{d’} \end{align*}$$
即\(\mathbf{X}\mathbf{X}^\top\boldsymbol{w}_{i}=\lambda_{i} \boldsymbol{w}_{i}\),这样可以更清楚的看出,\(\mathbf{W}\)为\(d’\)个\(\mathbf{X}\mathbf{X}^\top\)特征向量组成的矩阵,而\(\mathbf{\Lambda}\)为\(d’\)个\(\mathbf{X}\mathbf{X}^\top\)特征值组成的矩阵,特征值在主对角线上,其余位置为\(0\)。
那么,到底是哪些特征值,以及对应的特征向量呢?我们将\( \mathbf{X}\mathbf{X}^\top\mathbf{W}=\mathbf{W}\mathbf{\Lambda}\)入目标函数,即:
$$ \max_{\mathbf{W}} \mathrm{Tr}\left(\mathbf{W}^\top\mathbf{X}\mathbf{X}^\top\mathbf{W} \right)=\max_{\mathbf{\Lambda}} \mathrm{Tr}\left(\mathbf{\Lambda} \right)=\max_{\mathbf{\Lambda}} \sum_{i=1}^{d’}\lambda_i $$
可以看出,我们需要的是最大的\( d’\)特征值及其对应的特征向量。
至此我们可以下结论了,当我们将数据集从\( d\)降到\( d’\)时,需要找到矩阵\( \mathbf{X}\mathbf{X}^\top\)大的\( d’\)特征值,还有其对应的\( d’\)特征向量,这\( d’\)特征向量组成的矩阵\( \mathbf{W}\)是我们需要的矩阵!而且很容易发现,在数据已进行中心化处理后,这个矩阵\( \mathbf{X}\mathbf{X}^\top\)就是样本的散布矩阵吗?!(有些地方说是协方差矩阵,其实不严谨,协方差矩阵前面还要加一个常数项\( \frac{1}{n-1}\)不过这不影响推导)
因此我们进行主成分分析时,只需要求出样本协方差矩阵的特征值和特征向量就好了啊(通常在PCA中使用的是协方差矩阵,因为协方差矩阵提供了归一化的度量,这使得主成分的解释更为直观)。(´;ω;`)
1.2 基于最大可分性
基于最大可分性,或者说基于最大投影方差,就是当我们将所有样本点投影之后,它们尽可能分开。也就是说,我们应该使投影后的样本点方差最大化。我们知道,降维后样本的协方差矩阵为\( \frac{1}{n-1}\sum_{i=1}^n\boldsymbol{z}_i \boldsymbol{z}_i^\top\)其中对角线上的元素代表了样本点每一个维度的方差,我们要使得样本方差和最大化,也就变成了下面的优化目标:
$$\begin{align*}\max_{\mathbf{Z}} \mathrm{Tr}\left(\sum_{i=1}^n\boldsymbol{z}_i \boldsymbol{z}_i^\top \right)&=\max_{\mathbf{W}} \mathrm{Tr}\left(\sum_{i=1}^n\mathbf{W}^\top\boldsymbol{x}_i\boldsymbol{x}_i^\top\mathbf{W} \right) \\&=\max_{\mathbf{W}} \mathrm{Tr}\left(\mathbf{W}^\top\mathbf{X}\mathbf{X}^\top\mathbf{W} \right) \tag{1.3}\end{align*}$$
可以看到,从最大方差和的角度推导最终与最小重构距离的结果一致,即优化目标\( (1.3)\)\( (1.1)\)样!也就是说,他们优化目标实际上是同一个东西。同时,约束条件也是\( \mathbf{W}^\top\mathbf{W}=\mathbf{I}\)因此,我们可以得到相同的结果,基于最小投影距离得出的结论并非巧合:我们需要的是样本协方差矩阵的最大的\( d’\)特征值与对应的特征向量。相比较上面的推导这个容易多了(/゚Д゚)/,但是个人觉得还是距离比较直观。
2 PCA算法步骤
通过第一节的推导,我们可以总结出PCA的算法步骤:
输入:
- 样本集 \( \mathbf{X}=\left[{\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_n}\right]\);
- 低维子空间的维度 \( d’\)。
过程:
- 对所有样本进行中心化:\( \displaystyle \boldsymbol{x}_i\gets \boldsymbol{x}_i – \dfrac1m\sum_{i=1}^n \boldsymbol{x}_i\);
- 计算样本的协方差矩阵\( \dfrac{1}{n-1}\mathbf{X}\mathbf{X}^\top\);
- 对协方差矩阵\( \dfrac{1}{n-1}\mathbf{X}\mathbf{X}^\top\) 特征值分解(或者 奇异值分解);
- 取最大的\( d’\)特征值所对应的特征向量\( \boldsymbol{w}_1,\boldsymbol{w}_2,\dots,\boldsymbol{w}_{d’}\)并组成投影方向矩阵\( \mathbf{W}=[\boldsymbol{w}_1,\boldsymbol{w}_2,\dots,\boldsymbol{w}_{d’}]\);
- 对样本集中的每一个样本\( \boldsymbol{x}_i\)转化为新的样本\( \boldsymbol{z}_i=\mathbf{W}^\top \boldsymbol{x}_i\)。
输出:
- 降维后的样本集 \( \mathbf{Z}=\left[{\boldsymbol{z}_1,\boldsymbol{z}_2,\dots,\boldsymbol{z}_n}\right]\)。
有时候,我们还可以通过设置一个重构阈值\( t\)选取使下式成立的最小\( d’\): $$ \frac{\displaystyle \sum_{i=1}^{d’}\lambda_i}{\displaystyle \sum_{i=1}^{d}\lambda_i}\geq t $$ 左项也通常称为累计方差贡献率。
3 PCA算法实现
这里演示两种方法,一种是通过手动执行PCA算法步骤来计算,一种是利用scikit-learn库来计算PCA。
3.1 手动实现算法
import numpy as np
from sklearn.decomposition import PCA
# 原始数据:每列是一个学生(样本),每行是一个科目(特征)
X = np.array([
[95, 91, 88, 70, 75, 80, 78, 65, 85, 90], # 数学
[90, 87, 85, 65, 70, 76, 73, 60, 80, 88], # 物理
[76, 82, 70, 85, 88, 84, 80, 70, 74, 73], # 历史
[78, 78, 75, 80, 82, 79, 81, 73, 77, 76], # 地理
[85, 84, 83, 79, 80, 82, 81, 72, 84, 86], # 生物
])
# 转置为 (n_samples, n_features):每行是一个学生,每列是一个科目
X = X.T # shape: (10, 5)
# 设置保留的主成分维度
d_components = 2
# 初始化并拟合 PCA 模型
pca = PCA(n_components=d_components)
X_pca = pca.fit_transform(X)
# 输出结果
print("---使用 sklearn 库实现主成分分析(PCA)结果---")
print(f"原始数据形状:{X.shape}")
print(f"降维后形状:{X_pca.shape}")
print(f"前 {d_components} 个主成分累计方差贡献率:{np.sum(pca.explained_variance_ratio_):.5f}")
print("各同学在主成分空间中的表示(每行为一个样本):")
student_names = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J']
for i, vec in enumerate(X_pca):
vec_str = ', '.join(f"{v:.4f}" for v in vec)
print(f"{student_names[i]} → [{vec_str}]")---手动实现主成分分析(PCA)结果---
原始数据形状:(10, 5)
降维后形状:(10, 2)
前 2 个主成分累计方差贡献率:0.98843
各同学在主成分空间中的表示(每行为一个样本):
A → [-18.6833, 0.0872]
B → [-12.9775, 4.9490]
C → [-10.8687, -7.5310]
D → [17.8949, 5.1740]
E → [11.2636, 9.3748]
F → [2.7245, 5.5646]
G → [5.9531, 2.2502]
H → [24.4551, -12.8238]
I → [-5.1170, -3.3898]
J → [-14.6446, -3.6552]我们可以通过matplotlib库来将其可视化,并将新的标准正交基也投影到主成分空间,箭头的长度说明该特征在主成分空间中贡献。
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'SimHei' # 设置中文字体
plt.rcParams['axes.unicode_minus'] = False # 正常显示负号
feature_names = ['数学', '物理', '历史', '地理', '生物']
# 绘制散点图
plt.figure(figsize=(8, 6))
plt.scatter(X_pca[:, 0], X_pca[:, 1], color='skyblue', s=100, edgecolors='k')
student_names = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J']
for i, name in enumerate(student_names):
plt.text(X_pca[i, 0] + 0.5, X_pca[i, 1], name, fontsize=12)
# 添加主成分箭头
for i in range(len(feature_names)):
# 取前两个主成分分量(x, y)
x, y = top_eigenvectors[i, 0], top_eigenvectors[i, 1]
plt.arrow(0, 0, x * 10, y * 10, color='red', alpha=0.8, head_width=0.5, length_includes_head=True)
plt.text(x * 11, y * 11, feature_names[i], color='red', fontsize=12)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('Students projected in PCA space')
plt.axis('equal')
plt.grid(True, color='lightgray', linestyle='--', linewidth=0.5)
plt.axhline(0, color='gray', linewidth=0.5)
plt.axvline(0, color='gray', linewidth=0.5)
plt.tight_layout()
plt.show()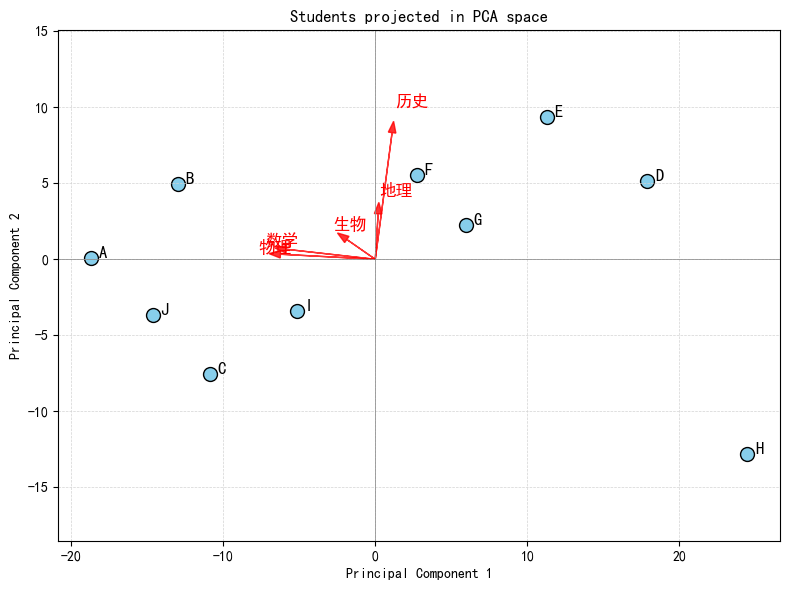
3.2 利用sklearn库实现算法
import numpy as np
from sklearn.decomposition import PCA
# 原始数据:每列是一个学生(样本),每行是一个科目(特征)
X = np.array([
[95, 91, 88, 70, 75, 80, 78, 65, 85, 90], # 数学
[90, 87, 85, 65, 70, 76, 73, 60, 80, 88], # 物理
[76, 82, 70, 85, 88, 84, 80, 70, 74, 73], # 历史
[78, 78, 75, 80, 82, 79, 81, 73, 77, 76], # 地理
[85, 84, 83, 79, 80, 82, 81, 72, 84, 86], # 生物
])
# 转置为 (n_samples, n_features):每行是一个学生,每列是一个科目
X = X.T # shape: (10, 5)
# 设置保留的主成分维度
d_components = 2
# 初始化并拟合 PCA 模型
pca = PCA(n_components=d_components)
X_pca = pca.fit_transform(X)
# 输出结果
print("---使用 sklearn 库实现主成分分析(PCA)结果---")
print(f"原始数据形状:{X.shape}")
print(f"降维后形状:{X_pca.shape}")
print(f"前 {d_components} 个主成分累计方差贡献率:{np.sum(pca.explained_variance_ratio_):.5f}")
print("各同学在主成分空间中的表示(每行为一个样本):")
student_names = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J']
for i, vec in enumerate(X_pca):
vec_str = ', '.join(f"{v:.4f}" for v in vec)
print(f"{student_names[i]} → [{vec_str}]")---使用 sklearn 库实现主成分分析(PCA)结果---
原始数据形状:(10, 5)
降维后形状:(10, 2)
前 2 个主成分累计方差贡献率:0.98843
各同学在主成分空间中的表示(每行为一个样本):
A → [-18.6833, -0.0872]
B → [-12.9775, -4.9490]
C → [-10.8687, 7.5310]
D → [17.8949, -5.1740]
E → [11.2636, -9.3748]
F → [2.7245, -5.5646]
G → [5.9531, -2.2502]
H → [24.4551, 12.8238]
I → [-5.1170, 3.3898]
J → [-14.6446, 3.6552] 可以看到,这和我们手动实现PCA算法的结果一致。值得注意的是,在进行主成分分析时,特征向量的符号是任意的,因为特征向量和其负数都指向相同的主成分轴。sklearn对奇异分解结果进行了一个处理,因为\(u_i\sigma_iv_i=(-u_i)\sigma_i(-v_i)\),也就是\(u\)和\(v\)同时取反得到的结果是一样的,而这可能会导致通过PCA降维得到不一样的结果(虽然都是正确的)。
4 PCA算法小结
主要优点:
- PCA仅仅需要以方差衡量信息量,不受数据集以外的因素影响;(也就是说它是一种无监督学习技术)
- 各主成分之间正交,可消除原始数据成分间的相互影响的因素;
- 计算方法简单,主要运算是特征值分解(或奇异值分解),易于实现。
主要缺点:
- 主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强;
- 方差小的非主成分也可能含有对样本差异的重要信息,因降维丢弃可能对后续数据处理有影响。

Ciallo~(∠・ω< )⌒☆